Relational Algebra - An Intro of it's Use and Operators

Consider the following database scenario:
You are planning a high school graduation party for the school. You keep data on those who have registered to be present on that day. We have students(S), teachers(T), staff members(SM), parents(P), and siblings(C) of the students, followed by relatives(F), and a list of registered people for the party(R). We also have information about food allergies(A). If we were asked to find out the group of people who is a 25 years old or older and a parent of a student who has a peanut allergy, what would you query?

SELECT S.name
FROM S
WHERE S.allergy='peanut' and S.parent=
               (SELECT P.name
                FROM P
                WHERE P.age >= 25)

As we can see here this is not the simplest query. Imagine if we had to query for something way more complex than this. Would you sit there and try things out until you got the right query? Would a database always have someone behind it entering queries? Not always(Probably not). It can be done of course, but there's a better solution for this.

Relational Algebra: relational algebra is a way of expressing relations. Just like algebra is a way of expressing numbers and their relations, relational algebra is a way of expressing things in a database with their set of operators. It can also be used to describe constraints of a database, though we'll elaborate on that in another post.


Relational Operators: relational operators are analogous to arithmetic operators; they operate on a certain operand and describes the operands' relationship to each other. Below we will jump into some of the basic operators.

1. Selection(σ): Like in SQL queries we are selecting a subset of rows from a relation(operand)
2. Projection(π): Keeps certain column(s) of a relation, I don't think this has an SQL counterpart
3. Cross-product(×): Also called Cartesian product. This takes relations and combines them
4. Join(⋈): Connects two relations with some sort of condition
5. Set-difference(−): an existing tuple(s) in one relation but nonexistent in another relation
6. Union(∪): Tuples that exist in one relation OR another relation. Realize that the "or" I'm talking about is logical or.
7. Intersection(∩): Tuples that exist in both of two relations
8. Renaming(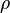): renames a relation or an attribute.

Operator Examples:
1. Selection(σ) & Projection(π): All of those who have a peanut allergy from the student list(S)
π_S.name(σ _{allergy='peanut'}(S))

3. Cross-product(×): All of those who have peanut allergy and are a student or teacher
π_S.name(σ _{allergy='peanut'}(S × T))

4. Join(⋈) All of those who have peanut allergy and are a student or teacher
π_S.name(σ _{allergy='peanut'}(S ⋈ T))

5. Set-difference(−): find the students who have an allergy but did not reserve a place for the party
π_S.name(σ _{allergy='peanut'}(S)) - π_S.name(R)

6. Union(∪) & Renaming(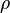): The list of students and teachers that have a name of "Sara"
π_R.name(σ _{R.name='sara'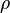}((R , (S ∪ T))))

7. Intersection(∩) & Renaming(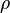): The list of people who's name is "sara" and is both a parent and a teacher
π_R.name(σ _{R.name='sara'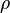} ((R , (P ∪ T))))